← Back to Start Page

Results¶

Introduction

Most approaches to Alpha Blending use a linear function to apply blending for an image. As part of testing, we explored other non-linear methods to determine if the image appeared more smooth compared to using a linear function. The non-linear functions that were tested are the
following:

• Cosine
• Quadratic
• Squareroot

Experiment Setup:
For this experiment, we have set the gamma value to 0.8 on each blending function.

Original Image

Original Image (Left)	Original Image (Right)

Linear Blending	Linear Graph

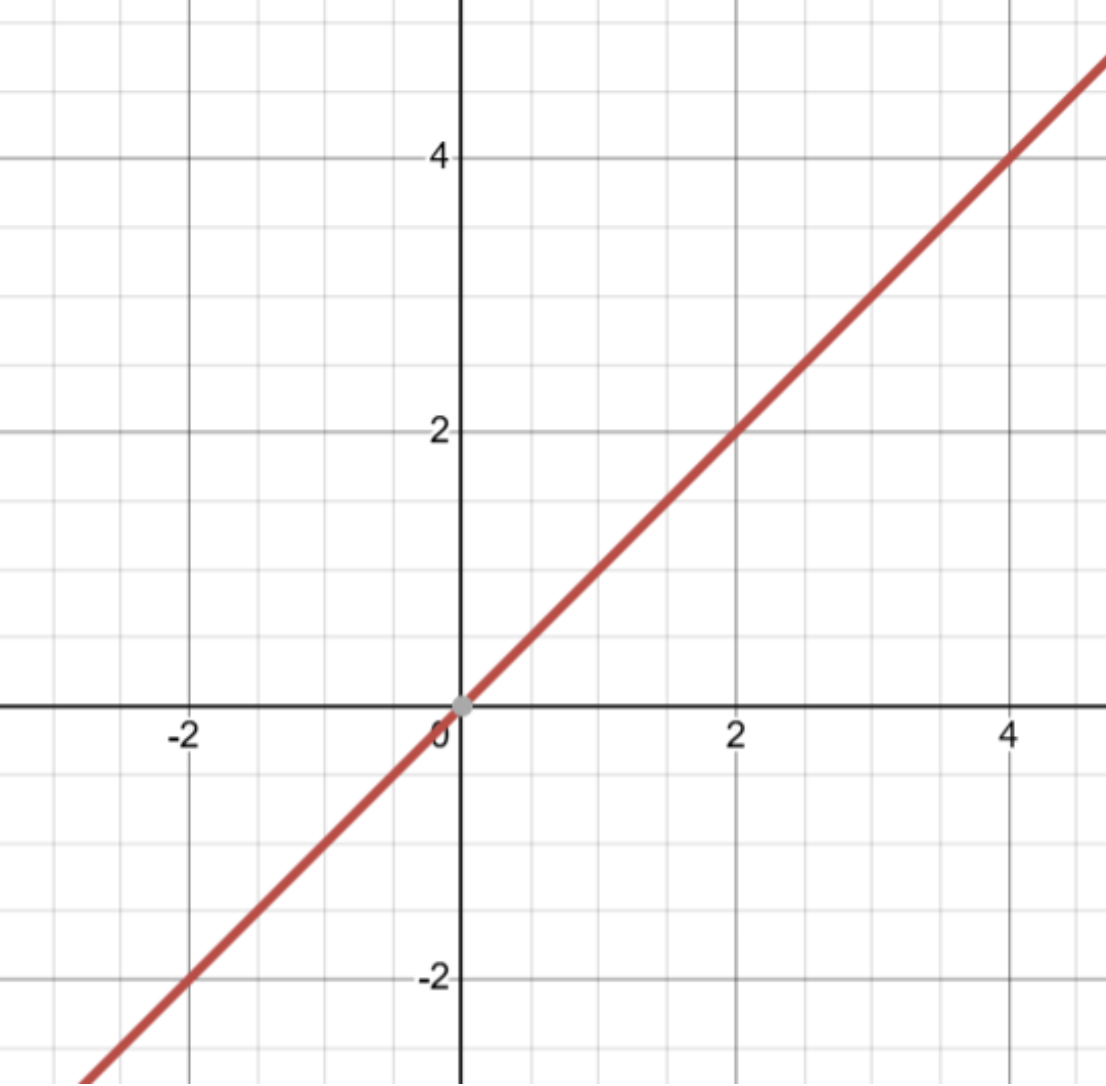Linear functions behavior is that of a straight line. For the left image, the origin represents the overlap starting point and as we move away from the overlap starting point, the Alpha blending is applied linearly. This behavior is mirrored on the right image. This image will be used to compare the other images generated from non-linear blending functions.

Cosine Blending	Cosine Graph

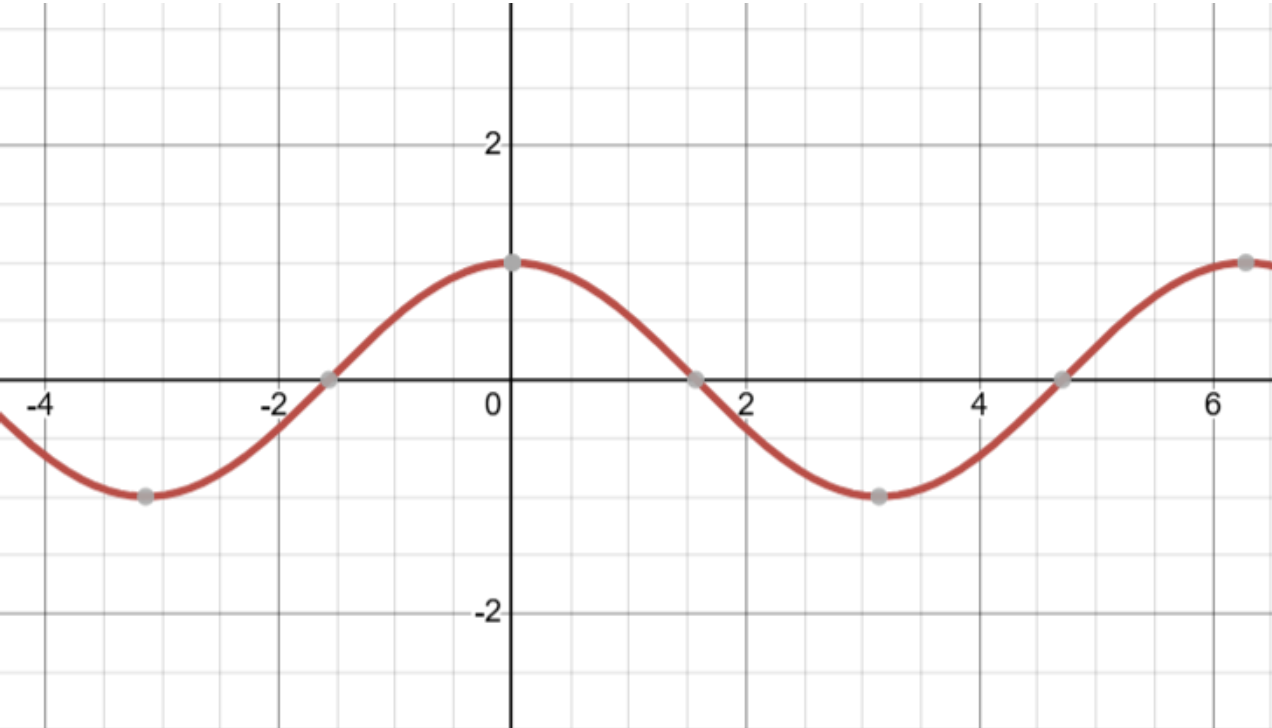The behavior of a cosine function provides a smooth and symmetric oscillation that transitions gradually between two states. In alpha blending, this results in a natural ease-in and ease-out effect, preventing abrupt changes in opacity and producing visually smooth. The smoothness of this image appears quite similar to the image using the linear function.

Quadratic Blending	Quadratic Graph

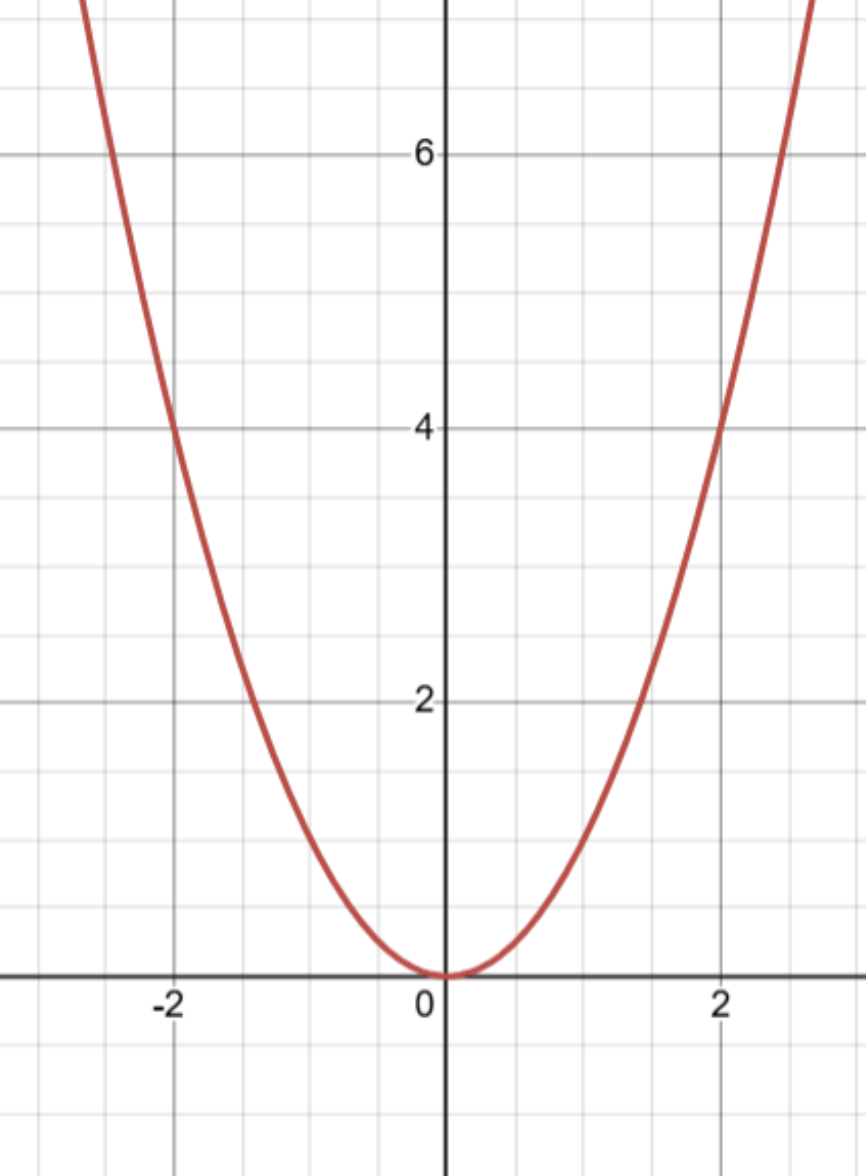The square root function produces a gradual-to-rapid transition, making it ideal for an ease-out alpha blend. The opacity changes slowly at first and then accelerates as the blend progresses, creating a natural-looking fade-in where the transition completes more. As a result though, it is easy to notice a light box appearing towards the middle of the overlap.

Squareroot Blending	Squareroot Graph

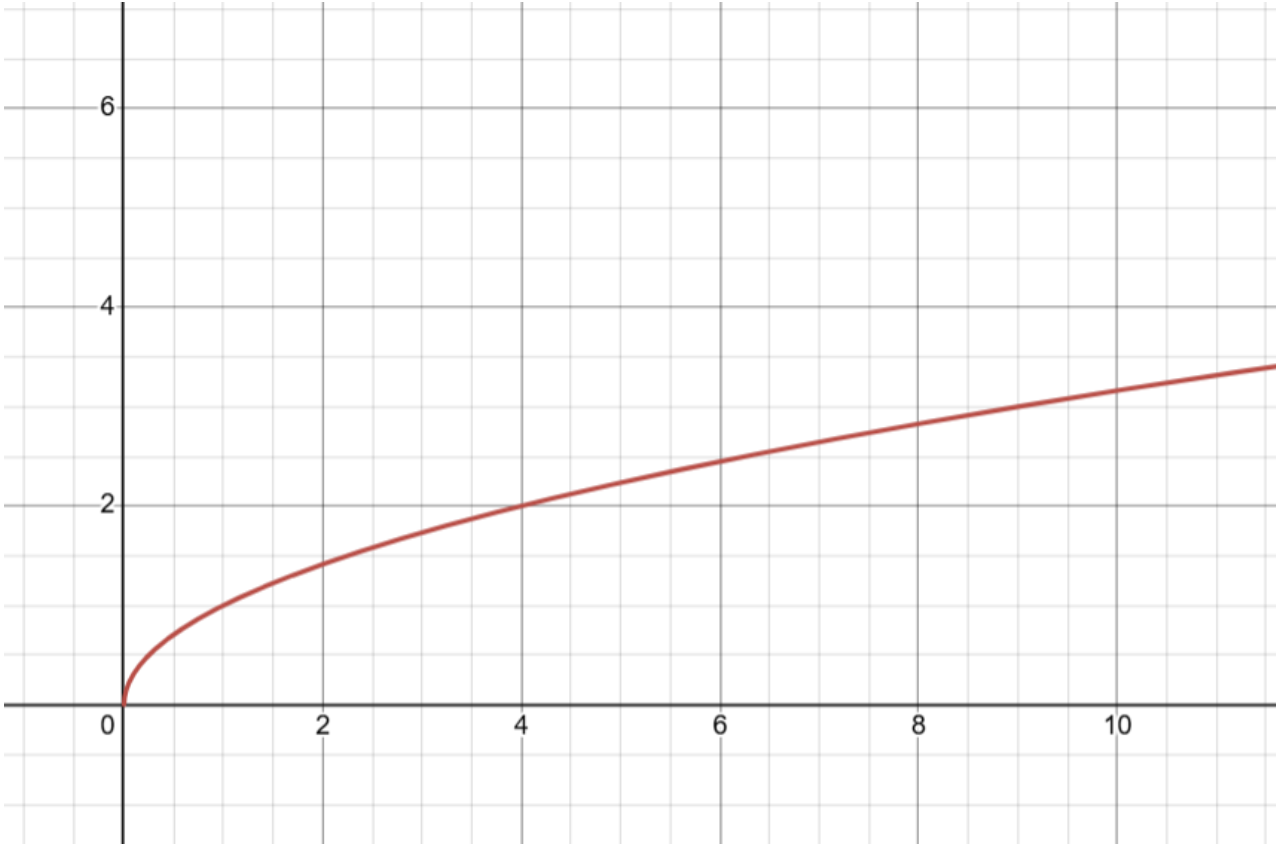The square root function in alpha blending produces a smooth, ease-out fade where opacity increases slowly at first and rapidly at the end. However, unlike quadratic blending, it tends to create a darker overlap region during the transition due to the slower growth of alpha values early in the blend.

Results

In conclusion, the results showed that each blending function produced distinct visual characteristics. The cosine function exhibited the most balanced and natural transition, behaving similarly to a linear blend but with smoother ease-in and ease-out effects, resulting in a visually pleasing fade. The quadratic function produces a gradual-to-rapid transition that looks smooth until the overlap, which had a light rectangle result. The square root function , on the other hand, displayed an ease-out behavior where the transition began slowly and accelerated toward the end, creating a darker overlap region due to the lower opacity values at the start of the blend . brightening the overlap area and emphasizing a stronger ease-in transition. Overall, the cosine function offered the most consistent and perceptually smooth blending, while the square root and quadratic functions highlighted how nonlinear curves can influence the perceived brightness and balance of an alpha blend.